
Which we can do in any order, since multiplication is commutative clearly, however you do it, it comes out to 16, not 1. I’ll include my own way of introducing the concept in a later post on why we need the rules.īut, continuing with an example: Translating these ideas into the case of multiplication and division, when we write It’s just Exponent-stuff, Multiplication-stuff, and Addition-stuff, with Parentheses acting as traffic cop, telling you when to do something other than what the signs say. Where some people memorize the rule as “Please Excuse My Dear Aunt Sally”, if I use a mnemonic at all, I make it PEMA: “Please Excuse My Attitude”. But we make the rules for people who aren't ready to see things in a mathematically mature way! (I myself prefer to avoid PEMDAS altogether, and teach the "rules" in a more natural way that leads into this mature perspective.) It's really wiser to think of subtraction as addition of the opposite, and division as multiplication by the reciprocal, and just leave D and S out of PEMDAS entirely, rather than try to fit them into the rules. That's not what the rule is supposed to mean, but many students don't get past the letters and see the meaning! I agreed with him: If you think that students have a tendency to misinterpret the rule, you're probably right but I think the reason is that PEMDAS is a poorly stated version of the rule, and it is easy to misunderstand it as meaning you do Multiplication, then Division, then Addition, then Subtraction. When doing multiplication and division from left to right, 8 / 2 * 4 = 4 * 4 = 16 When doing multiplication first, 8 / 2 * 4 = 8 / 8 = 1 I think they follow the PEMDAS rule BY THE LETTER, so they want to multiply before dividing. In telling students to "do multiplication and division IN THE ORDER THEY APPEAR," it seems they want to always do multiplication first. Here is a question from 2005 from a teacher, “WRW”: Confusion over Interpretation of PEMDAS This time I want to consider several kinds of misunderstandings we often see.
#Order of operations pemsa series#
Once students come to understand the order of operations through practice, only then may PEMDAS be introduced to serve its intended purpose: not as a set of instructions, but as a mnemonic device to assist with memory.Last time I started a series looking at the Order of Operations from various perspectives. Fortunately, I have a solution to this problem: rather than beginning a lesson on the order of operations by introducing PEMDAS, it should only be introduced after working through many examples using the four-step order of operations as it is written above. I have encountered far too many students who misunderstand the order of operations in precisely this way. This time, we have arrived at the correct solution. Next, we finish up by applying the fourth step, “evaluate addition and subtraction from left to right”: Since there are no parentheses or exponents, we will begin with the third step, “evaluate multiplication and division from left to right”: Let’s try our example again, this time using the order of operations.
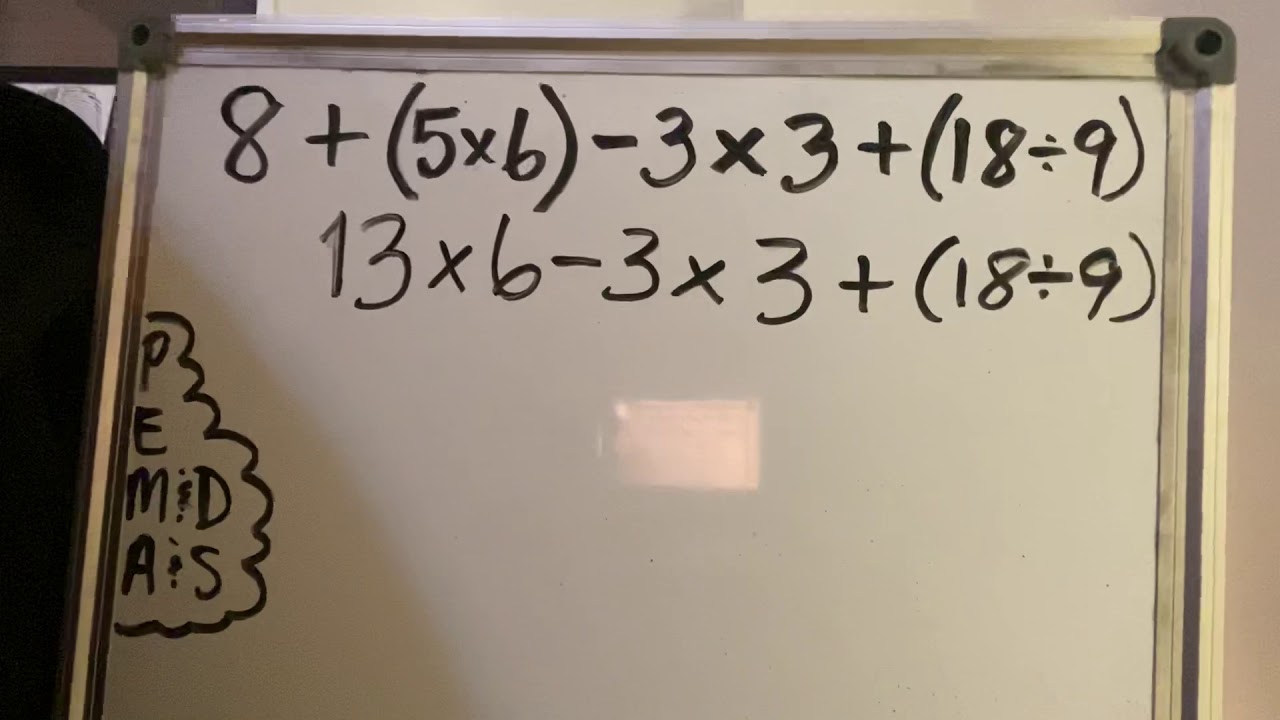
Importantly, multiplication and division are evaluated as part of the same step, as are addition and subtraction in the next step. In fact, the order of operations consists of four steps:Įvaluate multiplication and division from left to rightĮvaluate addition and subtraction from left to right

Or, that is what one would say if this solution were correct.įor many students, PEMDAS implies that the order of operations consists of six steps, one for each letter of the acronym. Next, these students would move on to division:Īn elegant solution! And all with the help of PEMDAS! What a wonderful invention! Since there are no parentheses or exponents, PEMDAS leads many students to think we should begin by evaluating multiplication.

Let’s take a look at a simple example: 4 - 3 + 10 ÷ 5 × 2. Or, rather, many students’ understanding of the order of operations is wrong and PEMDAS is to blame. This is great, right? These students remember the order of operations, right? Isn’t PEMDAS amazing? “Parentheses, Exponents, Multiplication, Division, Addition, Subtraction,” they say. Many of my middle- and high-school students remember PEMDAS, an acronym meant to represent the order of operations for evaluating mathematical expressions, from a previous class. “Please Excuse My Dear Aunt Sally,” they say (or “Please Eat My Doritos and Salsa,” one clever student told me).


 0 kommentar(er)
0 kommentar(er)
